In the simplest form, magnets are able to exert a force over a distance. Whether by inducing a field in a ferromagnetic material or interacting with another magnet, a magnet can exert a force without touching. The magnet’s magnetic field is the mechanism for this non-contact force.
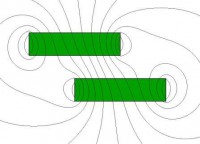When two magnets are attracting through a gap, are restrained from engaging, and are otherwise at equilibrium, then no force components are created, other than those trying to bring the magnets together. If one of the magnets is shifted, then the magnetic field “bends”, and “sideways” force components are established to maintain the equilibrium. This force acts to oppose the motion of the shifted magnet and to propagate the second magnet so that the system can remain in or achieve equilibrium again.
Additionally, there were “sideways” magnetic field components, and thereby, sideways force components before the shift; but they canceled out because there were an equal number acting in all directions. Hence the system was at equilibrium. When one magnet was shifted, the symmetry of the field was skewed, and the sideways field components became unbalanced, resulting in a net force to drive the system back to equilibrium.
These sideways force components are the mechanism that allows for Linear and Torque Magnetic Couplers to convey a force over a distance. While more prevalent, Torque Couplers are really Linear Couplers, but with rotational motion/geometry. The “linear force” is the force acting tangential to the rotational path of the system. The summation of the effective tangential acting forces for all magnet elements in the system multiplied by the mean radius of the system results in the effective torque.
(F1 + F2 +… Fn) x Radius = Effective Torque
(Where “F” is the force acting tangentially to the magnet’s rotational path for each array element up to “n” elements.)
As described above, force components are established by skewing the symmetry of the system. These force components are established by the bending of the magnetic field lines. The relative intensity of the force corresponds to the degree of flux line bending. The range is effectively zero for a system at equilibrium, to some maximum which depends upon the system’s geometry and the coupler design.
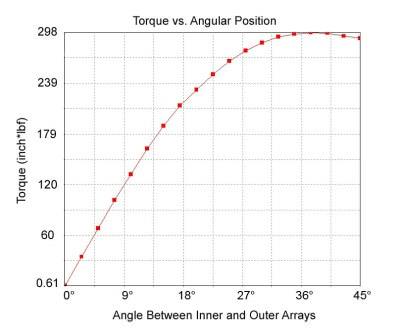Since there is a range, this would assert that there must be some relative motion (shift) before a linear force, or torque, is created. This motion is what we call the “pitch”, and it may need to be accounted for during the design. For instance, for a particular magnet torque coupler, the maximum torque may not be achieved until the system has rotated through 15°. This may or may not be an issue for some applications, but it must be observed that maximum torque and maximum linear force occur at the maximum system skew.
If the system is driven past this maximum skew, the Torque and Linear Coupler halves will “slip” and essentially decouple. The halves will not couple until all motion has ceased. Typically, Linear Couplers must be reset and forced back into the desired position. Linear Couplers, once decoupled, will oppose being coupled again.
We know that design, utility, and external variables are inextricably connected in many applications. Magnetic field torque and Linear Couplers are no different. Please contact Dura Magnetics to receive coupler selection and design assistance.